| На главную ↑ Выше |
Расчёт амплитудно-частотных характеристик |
| Заказать расчет |
На страницах:
Метод контурных токов
Метод узловых напряжений
были рассмотрены методы, которые можно использовать для расчёта амплитудно- и фазо- частотных характеристик любых линейных четырёхполюсников. Однако для многозвенных четырёхполюсников эти методы приводят к весьма громоздким вычислениям, поскольку связаны с решением уравнений высокого порядка. Существуют более простые методы расчёта АЧХ. Один из таких методов был рассмотрен на странице, которая помещена в архив. Метод сводился к расчёту коэффициентов передачи отдельных звеньев четырёхполюсника путём вычисления параллельных и последовательных сопротивлений и не требовал составления уравнений. Т.е. он был более инженерным и более простым.
Ниже мы рассмотрим ещё более простой метод и приведем примеры программ для типовых фильтров.
Элементы теории
Под амплитудно-частотной характеристикой (АЧХ) обычно понимается соотношение между выходным и входным напряжением четырёхполюсника, которое называется коэффициентом передачи:
K(f) = Un(f) / E(f)
Здесь Un(f) и E(f) - выходное и входное напряжение соответственно, которые можно измерить физически, т.е. с помощью вольтметров V1 и V2 как показано на рис. 1.
| Рис.1 |
Соответственно K(f) - это действительное число, указывающее во сколько раз напряжение на выходе четырёхполюсника больше или меньше напряжения на его входе .
В теории существует также понятие комплексного коэффициента передачи:
K(f) = Un(f) / E(f)
Здесь жирный шрифт означает комплексную величину, которая учитывает не только соотношение амплитуд, но и сдвиг фазы гармонического напряжения. На практике, в большинстве случаев, основной интерес представляет амплитуда напряжения. В этом случае, если известно K(f), то K(f) вычисляется как модуль комплексного числа:
K(f) = | K(f) |
При необходимости от K(f) можно определить так же и фазо-частотную характеристику, которая будет рассмотрена на другой странице.
Рассмотрим расчёт АЧХ на примере простейшей интегрирующей RC-цепочки:
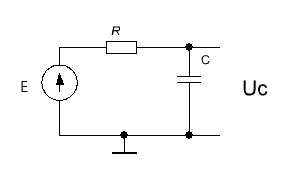 |
| Рис.2 |
Как видим, RC-цепочка это простой делитель напряжения, хотя и частотно зависимый. Передаточная функция определяется как:
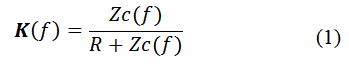 |
Комплексное сопротивление ёмкости: Zс = -i/ωC, где i - мнимая единица, ω = 2πf - круговая частота.
Подставив эти значения, приведём формулу к следующему виду:
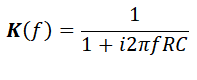 |
Отсюда находим коэффициент передачи как модуль передаточной функции:
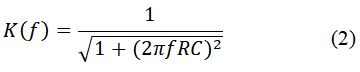 |
Из формулы следует, что при f = 0, K(0) = 1, а с ростом частоты значения K(f) уменьшаются. Это означает, что данная RC-цепь обладает свойствами фильтра нижних частот. Из формулы нетрудно определить частоту среза данного фильтра - т.е. частоту fc при которой коэффициент передачи равен K(fc) = 1 /√2:
fc = 1/2πRC
Зададим номиналы: R = 1 кОм , С = 1 мкФ и при помощи формы определим: fc = ~ 160 Гц. Теперь перейдём непосредственно к расчёту АЧХ, используя формулу (2) и калькулятор KAN.
Ниже представлен текст соответствующей программы, которую нужно ввести в окно калькулятора и нажать кнопку "Вычислить".
; Калькулятор KAN. http://калькулятор.нехаев.рф/calc/calculator.html
; расчёт АЧХ RC-фильтра нижних частот при заданных R и C
; по аналитической формуле
C = 1E-6; ёмкость в Фарадах
R = 1000 ; сопротивление в Омах
;цикл расчета АЧХ фильтра
[ f = 10 : 1000, 10 ; пределы цикла f_min : f_max, f_step
K = 1/sqr( 1 + (2*pi*f*R*C)^2) ; коэфф передачи
K_dB = 20*lg(K) ; коэфф передачи в децибелах
val(f,K_dB); вывод данных в таблицу и на график
] ; завершение цикла
grafY(-20,0) ; пределы по оси Y
grafX(0,1000) ; пределы по оси X
; расчёт АЧХ RC-фильтра нижних частот при заданных R и C
; по аналитической формуле
C = 1E-6; ёмкость в Фарадах
R = 1000 ; сопротивление в Омах
;цикл расчета АЧХ фильтра
[ f = 10 : 1000, 10 ; пределы цикла f_min : f_max, f_step
K = 1/sqr( 1 + (2*pi*f*R*C)^2) ; коэфф передачи
K_dB = 20*lg(K) ; коэфф передачи в децибелах
val(f,K_dB); вывод данных в таблицу и на график
] ; завершение цикла
grafY(-20,0) ; пределы по оси Y
grafX(0,1000) ; пределы по оси X
Результатом будут таблица и график АЧХ в децибелах, который показан ниже:
Строка:
K = 1/sqr( 1 + (2*pi*f*R*C)^2) ; коэфф передачи- это программный код, соответствующий формуле (2).
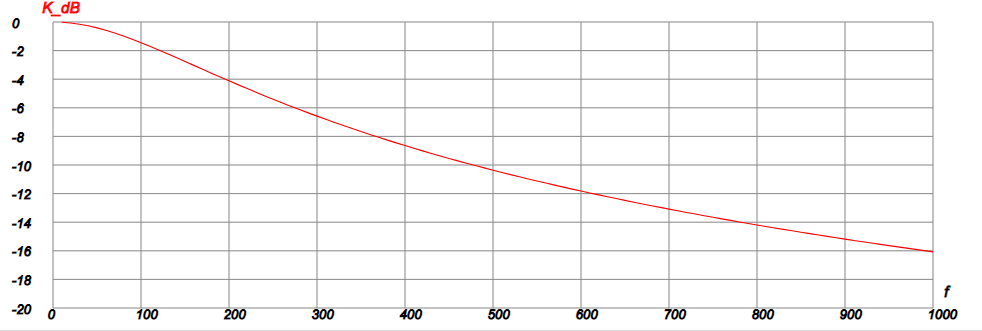 |
| Рис. 3 |
График представлен, как это обычно принято, в децибелах, где
K(f)db = 20Lg K(f)
Внизу страницы в Приложении 1 приводится аналогичная программа, составленная в среде Mathcad.
Рассмотренный подход расчёта АЧХ можно назвать аналитическим, т.к. мы вывели аналитическую формулу (2), по которой затем и произвели расчёт. Однако такой подход применим только для простых схем, содержащих небольшое число элементов. Ниже мы рассмотрим более универсальный подход, основанный на возможностях калькулятора KAN производить вычисления с комплексными числами.
Cнова рассмотрим схему RC-цепи на рис. 2 и соответствующую ей формулу комплексного коэффициента передачи (1). Составим также программу для расчёта АЧХ с использованием комплексных вычислений:
; Калькулятор KAN. http://калькулятор.нехаев.рф/calc/calculator.html
; расчёт АЧХ RC-фильтра нижних частот при заданных R и C
; по комплексным коэффициентам передачи
C = 1E-6; ёмкость в Фарадах
R = 1000 ; сопротивление в Омах
;цикл расчета АЧХ фильтра
[ f = 10 : 1000, 10 ; пределы цикла f_min : f_max, f_step
w = 2*pi*f ; круговая частота
ZC = -!/(w*C) ; комплексное сопротивление ёмкости C
K = ZC/(R + ZC ) ; комплексный коэффициент передачи
K = modC (K) ; модуль коэффициента передачи
K_dB = 20*lg(K) ; коэфф передачи в децибелах
val(f,K_dB); вывод данных в таблицу и на график
] ; завершение цикла
grafY(-20,0) ; пределы по оси Y
grafX(0,1000) ; пределы по оси X
; расчёт АЧХ RC-фильтра нижних частот при заданных R и C
; по комплексным коэффициентам передачи
C = 1E-6; ёмкость в Фарадах
R = 1000 ; сопротивление в Омах
;цикл расчета АЧХ фильтра
[ f = 10 : 1000, 10 ; пределы цикла f_min : f_max, f_step
w = 2*pi*f ; круговая частота
ZC = -!/(w*C) ; комплексное сопротивление ёмкости C
K = ZC/(R + ZC ) ; комплексный коэффициент передачи
K = modC (K) ; модуль коэффициента передачи
K_dB = 20*lg(K) ; коэфф передачи в децибелах
val(f,K_dB); вывод данных в таблицу и на график
] ; завершение цикла
grafY(-20,0) ; пределы по оси Y
grafX(0,1000) ; пределы по оси X
Ниже приведён фрагмент программы, где вычисляются коэффициенты передачи
K = ZC/(R + ZC ) ; комплексный коэффициент передачи K = modC (K) ; модуль коэффициента передачи K_dB = 20*lg(K) ; коэфф передачи в децибелахПервая строка соответствует формуле (1) и вычисляет комплексный коэффициент передачи. Вторая строка - взятие модуля комплексного числа. Третья - перевод в децибелы. Если ввести текст программы в окно калькулятора, то получим график идентичный тому, что на рис. 3. Строка:
ZC = -!/(w*C) ; комплексное сопротивление ёмкостисоответствует математической записи: Zc = -i/ωC, где i - мнимая единица.
Внизу страницы в Приложении 2 приводится аналогичная программа, составленная в среде Mathcad.
Расчёт АЧХ сложных схем
Расммотрим обобщённую схему линейной цепи т.н. лестничной структуры. По этой структуре могут быть реализованы фильтры (нижних и верхних частот, полосовые, режекторные), содержащие элементы L, C и R.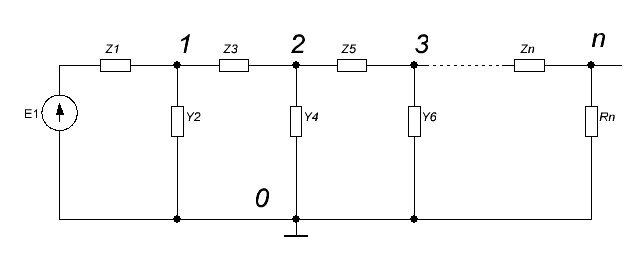 |
| Рис. 4 |
Из теории известно, что коэффицент передачи такого 4-х полюсника может быть описан следующими выражениями:
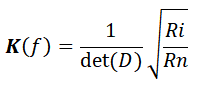 |
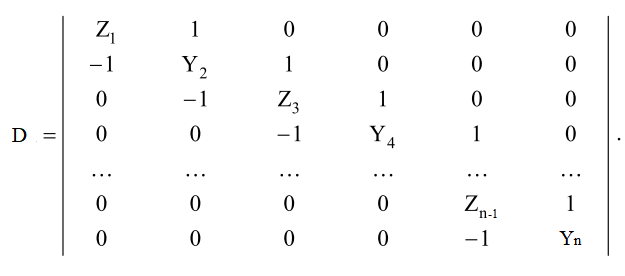 |
где D - матрица, состоящая из элементов рассмотренной схемы, det(D) - детерминант этой матрицы, Ri и Rn сопротивления источника и нагрузки соответственно.
Теперь рассмотрим реальную схему LC-фильтра нижних частот третьего порядка:
| Рис. 5 |
Для частоты среза 100 Гц и C = 10 мкФ (10E-6 Ф) расчётом по форме получено:
L1 = L2 = 0.5 Гн (L/2)
Rn = Ri = 318 Ом
Ниже приведена программа расчёта АЧХ данного фильтра:
; Калькулятор KAN. http://калькулятор.нехаев.рф/calc/calculator.html
; расчёт АЧХ LC-фильтра нижних частот 3-го порядка
; матричный метод
mas: D[4,4] ; резервирование массива под матрицу
C = 10E-6; ёмкость в Фарадах
Ri = 318; сопротивление в Омах
Rn = Ri
L1 = 0.5
L2 = L1
;цикл расчета АЧХ фильтра
[ f = 10 : 1000, 10 ; пределы цикла f_min : f_max, f_step
w = 2*pi*f ; круговая частота
ZC = -!/(w*C) ; комплексное сопротивление ёмкости
ZL1 = !(w*L1) ; комплексное сопротивление индуктивности
ZL2 = ZL1
;параметры матрицы
Z1 = Ri + ZL1
Z3 = ZL2
Y2 = 1/ZC ; комплексная проводимость ёмкости
Y4 = 1/Rn
; матрица
D=|
Z1 1 0 0
-1 Y2 1 0
0 -1 Z3 1
0 0 -1 Y4
|
det = detM(D) ; определитель матрицы
K = 1/det*sqr(Ri/Rn) ; комплексный коэффициент передачи фильтра
K = modC (K) ; модуль коэффициента передачи
K_dB = 20*lg(K) ; коэфф передачи в децибелах
val(f,K_dB); вывод данных в таблицу и на график
] ; завершение цикла
grafY(-30,0) ; пределы по оси Y
grafX(0,400) ; пределы по оси X
; расчёт АЧХ LC-фильтра нижних частот 3-го порядка
; матричный метод
mas: D[4,4] ; резервирование массива под матрицу
C = 10E-6; ёмкость в Фарадах
Ri = 318; сопротивление в Омах
Rn = Ri
L1 = 0.5
L2 = L1
;цикл расчета АЧХ фильтра
[ f = 10 : 1000, 10 ; пределы цикла f_min : f_max, f_step
w = 2*pi*f ; круговая частота
ZC = -!/(w*C) ; комплексное сопротивление ёмкости
ZL1 = !(w*L1) ; комплексное сопротивление индуктивности
ZL2 = ZL1
;параметры матрицы
Z1 = Ri + ZL1
Z3 = ZL2
Y2 = 1/ZC ; комплексная проводимость ёмкости
Y4 = 1/Rn
; матрица
D=|
Z1 1 0 0
-1 Y2 1 0
0 -1 Z3 1
0 0 -1 Y4
|
det = detM(D) ; определитель матрицы
K = 1/det*sqr(Ri/Rn) ; комплексный коэффициент передачи фильтра
K = modC (K) ; модуль коэффициента передачи
K_dB = 20*lg(K) ; коэфф передачи в децибелах
val(f,K_dB); вывод данных в таблицу и на график
] ; завершение цикла
grafY(-30,0) ; пределы по оси Y
grafX(0,400) ; пределы по оси X
На рис. 6 показан график АЧХ данного фильтра:
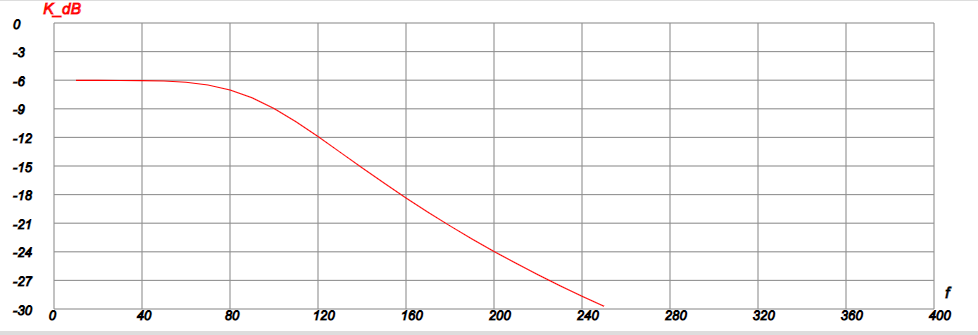 |
| Рис. 6 |
Видно, что на частоте 100 Гц коэффициент передачи равен -9 дБ или -3 дБ относительно нулевой частоты.
Программу можно скопировать и выполнить на калькуляторе КАН.
В заключение рассмотрим популярный в своё время фильтр на частоту среза 3000 Гц с весьма крутым срезом и значительным затуханием в полосе непропускания:
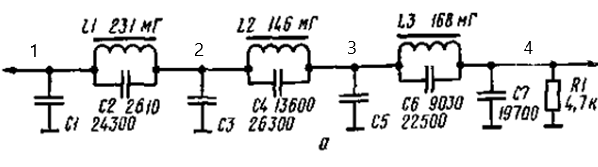 |
| Рис. 7 |
Программа приведена ниже:
; Калькулятор KAN. http://калькулятор.нехаев.рф/calc/calculator.html
; расчёт АЧХ LC-фильтра нижних частот с крутым срезом
; матричный метод
; ёмкости в Ф
mas: D[8,8]
C1 = 24300E-12
C2 = 2610E-12
C3 = 26300E-12
C4 = 13600E-12
C5 = 22500E-12
C6 = 9030E-12
C7 = 19700E-12
; индуктивности в Гн
L1 = 231E-3
L2 = 146E-3
L3 = 168E-3
;
Rn = 4700
Ri = Rn
;
;цикл расчета АЧХ фильтра
[ f = 100 : 10000, 50 ; пределы цикла f_min : f_max, f_step
w = 2*pi*f ; круговая частота
; комплексные сопротивления ёмкостей
ZC1 = -!/(w*C1)
ZC2 = -!/(w*C2)
ZC3 = -!/(w*C3)
ZC4 = -!/(w*C4)
ZC5 = -!/(w*C5)
ZC6 = -!/(w*C6)
ZC7 = -!/(w*C7)
; комплексные сопротивления индуктивностей
ZL1 = !(w*L1)
ZL2 = !(w*L2)
ZL3 = !(w*L3)
; параметры матрицы
Z1 = Ri
Y2 = 1/ZC1
Z3 = parC(ZL1,ZC2)
Y4 = 1/ZC3
Z5 = parC(ZL2,ZC4)
Y6 = 1/ZC5
Z7 = parC(ZL3,ZC6)
Y8 = 1/parC(Rn,ZC7)
D = |
Z1 1 0 0 0 0 0 0
-1 Y2 1 0 0 0 0 0
0 -1 Z3 1 0 0 0 0
0 0 -1 Y4 1 0 0 0
0 0 0 -1 Z5 1 0 0
0 0 0 0 -1 Y6 1 0
0 0 0 0 0 -1 Z7 1
0 0 0 0 0 0 -1 Y8
|
;
det = detM(D); определитель матрицы
K = 1/det*sqr(Ri/Rn) ; комплексный коэффициент передачи фильтра
K = modC (K) ; модуль коэффициента передачи
K_dB = 20*lg(K) ; коэфф передачи в децибелах
val(f,K_dB); вывод данных в таблицу и на график
] ; завершение цикла
grafY(-100,0) ; пределы по оси Y
grafX(0,10000) ; пределы по оси X
; расчёт АЧХ LC-фильтра нижних частот с крутым срезом
; матричный метод
; ёмкости в Ф
mas: D[8,8]
C1 = 24300E-12
C2 = 2610E-12
C3 = 26300E-12
C4 = 13600E-12
C5 = 22500E-12
C6 = 9030E-12
C7 = 19700E-12
; индуктивности в Гн
L1 = 231E-3
L2 = 146E-3
L3 = 168E-3
;
Rn = 4700
Ri = Rn
;
;цикл расчета АЧХ фильтра
[ f = 100 : 10000, 50 ; пределы цикла f_min : f_max, f_step
w = 2*pi*f ; круговая частота
; комплексные сопротивления ёмкостей
ZC1 = -!/(w*C1)
ZC2 = -!/(w*C2)
ZC3 = -!/(w*C3)
ZC4 = -!/(w*C4)
ZC5 = -!/(w*C5)
ZC6 = -!/(w*C6)
ZC7 = -!/(w*C7)
; комплексные сопротивления индуктивностей
ZL1 = !(w*L1)
ZL2 = !(w*L2)
ZL3 = !(w*L3)
; параметры матрицы
Z1 = Ri
Y2 = 1/ZC1
Z3 = parC(ZL1,ZC2)
Y4 = 1/ZC3
Z5 = parC(ZL2,ZC4)
Y6 = 1/ZC5
Z7 = parC(ZL3,ZC6)
Y8 = 1/parC(Rn,ZC7)
D = |
Z1 1 0 0 0 0 0 0
-1 Y2 1 0 0 0 0 0
0 -1 Z3 1 0 0 0 0
0 0 -1 Y4 1 0 0 0
0 0 0 -1 Z5 1 0 0
0 0 0 0 -1 Y6 1 0
0 0 0 0 0 -1 Z7 1
0 0 0 0 0 0 -1 Y8
|
;
det = detM(D); определитель матрицы
K = 1/det*sqr(Ri/Rn) ; комплексный коэффициент передачи фильтра
K = modC (K) ; модуль коэффициента передачи
K_dB = 20*lg(K) ; коэфф передачи в децибелах
val(f,K_dB); вывод данных в таблицу и на график
] ; завершение цикла
grafY(-100,0) ; пределы по оси Y
grafX(0,10000) ; пределы по оси X
График АЧХ данного ФНЧ представлен на рис. 8
.
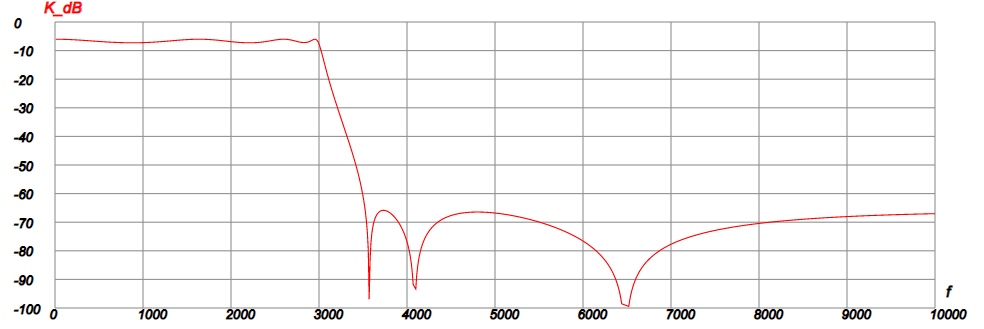 |
| Рис. 8 |
Судя по виду АЧХ, это т.н. эллиптический фильтр.
Программу так же можно скопировать и выполнить на калькуляторе КАН.
Её не трудно переделать для схемы линейного 4-х полюсника любой сложности. Однако оговоримся, что данный метод применим только к 4-х полюсникам, звенья которых соединены последовательно, тогда как прямые соединения звеньев через звено и больше отсутствуют (такие соединения характерны для мостовых 4-х полюсников). В этом случае воспользуйтесь методами контурных токов или узловых напряжений.
Приложение 1. Расчет АЧХ RC цепи по аналитической формуле на Mathcad
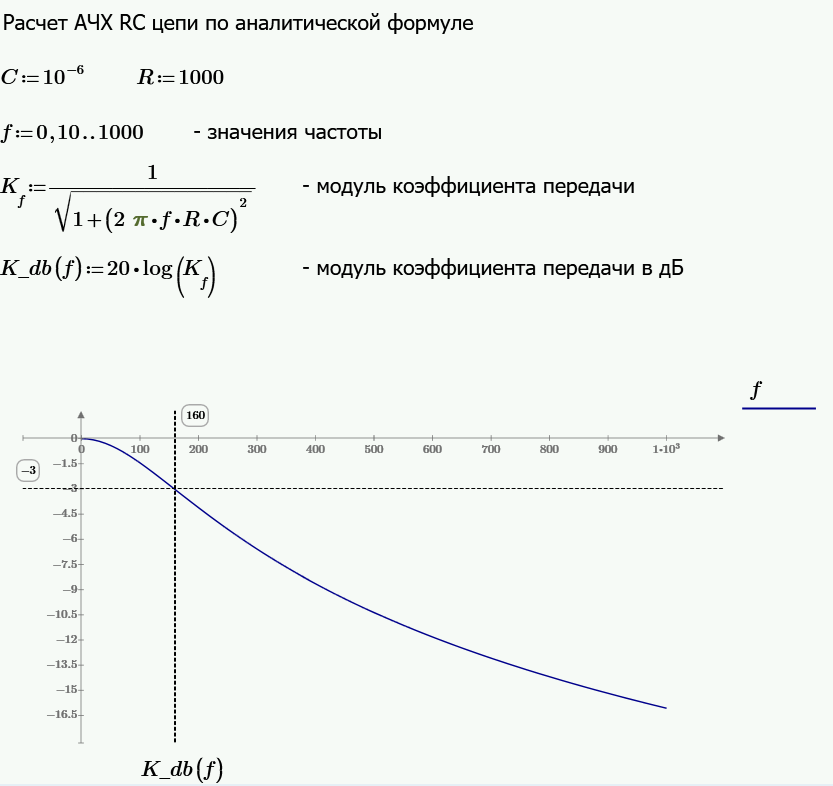
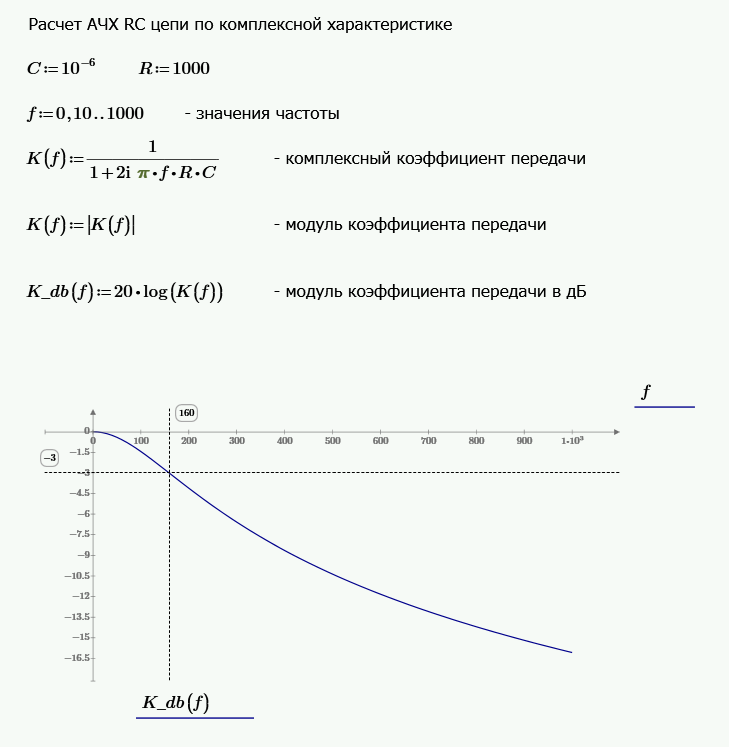
Приложение 2. Расчет АЧХ RC цепи по комплексной характеристике на Mathcad

|
Обратная связь: alexander.nekhaev53@gmail.com |

|
Поддержать проект |

|
Заказать расчет |